Ausgelöst durch Prüfungsvorbereitung und Schreiben an der Masterarbeit habe ich mich in letzter Zeit viel mit Typen formaler Grammatiken beschäftigt, die alle kontextfreien Sprachen beschreiben können und darüber hinaus einige, aber nicht alle kontextsensitiven Sprachen. Einen solchen Grammatikformalismus, nämlich Simple Range Concatenation Grammars (SRCG), habe ich in Teil 1 dieser Serie vorgestellt. In Teil 3 werde ich Anwendungen auf natürliche Sprache skizzieren.
Heute ist Teil 2 dran und damit die Vogelperspektive: Wo stehen wir auf der Chomsky-Hierarchie der formalen Sprachen? Ich kopiere dazu einfach Herrn Raus Übersicht über die Chomksy-Hierarchie, füge aber zwei weitere Stufen, also zwei weitere Klassen von Sprachen ein.
- Chomsky 0: Alle Sprachen, die sich überhaupt durch eine Grammatik beschreiben lassen.
- Chomsky 1: Eine Teilmenge davon, nämlich die Sprachen, die sich durch eine kontextsensitive Grammatik beschreiben lassen.
- PTIME aka P: Die Sprachen, bei denen das Wortproblem in Polynomialzeit entscheidbar ist. Range Concatenation Grammars (RCG) können genau diese Sprachen beschreiben. PTIME ist eine Teilmenge von Chomsky 0; ist es auch eine Teilmenge von Chomsky 1? Ich weiß es nicht, vielleicht weiß es auch niemand, aus dieser Übersicht geht es jedenfalls nicht hervor. Für Aufklärung bin ich dankbar.
- Eine Teilmenge sowohl von Chomksy 1 als auch von PTIME sind die Sprachen, die sich durch Simple Range Concatenation Grammars (SRCG) beschreiben lassen. So weit ich weiß, hat diese Klasse von Sprachen keinen einschlägigen Namen. SRCG ist eine eingeschränkte Variante von RCG, aber immer noch deutlich mächtiger als kontextfreie Grammatiken (CFG). Es gehört zu den so genannten „schwach kontextsensitiven“ (mildly context-sensitive) Grammatikformalismen, die vor allem im Zusammenhang mit natürlicher Sprache interessant sind – wo kontextfreie Grammatiken für eine adäquate Beschreibung nicht mehr ausreichen, man aber wegen Effizienz und Theoriedesign auch nicht zu weit darüber hinausgehen will. Dieselbe Klasse von Sprachen lässt sich durch die mit SRCG auch sonst so gut wie identischen Formalismen Linear Context-free Rewriting Systems (LCFRS) und Multiple Context-free Grammars (MCFG) beschreiben.
- Chomsky 2: Eine Teilmenge davon, nämlich die Sprachen, die sich durch eine kontextfreie Grammatik beschreiben lassen.
- Chomsky 3: Eine Teilmenge davon, nämlich die Sprachen, die sich durch eine reguläre Grammatik beschreiben lassen.
Die originale vierstufige Chomksy-Hierarchie bietet ein schönes Zwiebelschalenmodell, bei dem jede Sprachenmenge die nächste strikt einschließt:
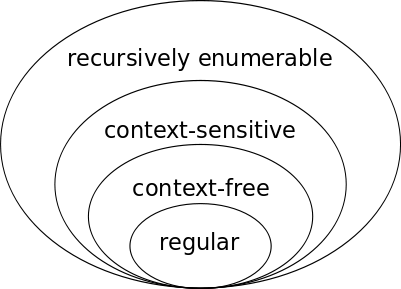 Diese Schönheit habe ich durch mein Unwissen, ob PTIME eine Teilmenge von Chomsky 1 ist, zerstört. Bedenkt man aber, dass Chomsky 1, also die Klasse der kontextsensitiven Sprachen, meines Wissens weder theoretisch noch praktisch besonders interessante Eigenschaften hat, kann man sie rausschmeißen und aus der obigen Auflistung durchaus wieder eine schöne Zwiebel basteln:
Diese Schönheit habe ich durch mein Unwissen, ob PTIME eine Teilmenge von Chomsky 1 ist, zerstört. Bedenkt man aber, dass Chomsky 1, also die Klasse der kontextsensitiven Sprachen, meines Wissens weder theoretisch noch praktisch besonders interessante Eigenschaften hat, kann man sie rausschmeißen und aus der obigen Auflistung durchaus wieder eine schöne Zwiebel basteln:
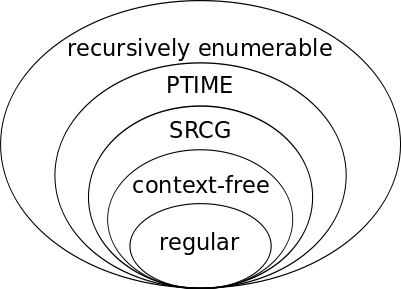 Doch Vorsicht: In einem Vortrag habe ich einmal ein entsprechendes Diagramm für die verschiedenen schwach kontextsensitiven Grammatikformalismen gesehen, die es heute so gibt. Es sah ungefähr so aus:
Doch Vorsicht: In einem Vortrag habe ich einmal ein entsprechendes Diagramm für die verschiedenen schwach kontextsensitiven Grammatikformalismen gesehen, die es heute so gibt. Es sah ungefähr so aus:
In Teil 3: Warum man arguably schwach kontextsensitive Grammatikformalismen braucht, um natürliche Sprache zu beschreiben.
Nachbemerkung 1: mildly context-sensitive klingt schwammig, ist aber relativ präzise definiert. Der Begriff bezieht sich im Gegensatz z.B. zu context-sensitive und context-free nicht auf Sprachen, sondern auf Mengen von Sprachen. Eine Menge von Sprachen ist schwach kontextsensitiv genau dann, wenn sie einerseits alle kontextfreien Sprachen enthält und überdies kreuzende Abhängigkeiten beschreiben kann (siehe dazu Teil 3), andererseits aber nur Sprachen enthält, die in polynomieller Zeit parsbar sind (also eine Teilmenge von PTIME ist) und überdies konstantes Wachstum aufweisen. Für Details siehe Joshi (1985) oder Kallmeyer (2010). Trotz dieser präzisen Definition gibt es noch keinen Grammatikformalismus, von dem man wüsste, dass er die größtmögliche schwach kontextsensitive Menge von Sprachen beschreibt. Obwohl SRCG nach heutigem Kenntnisstand der mächtigste schwach kontextsensitive Formalismus ist, kann es also gut sein, dass es eine schwach kontextsensitive Menge von Sprachen gibt, die Sprachen enthält, die SRCG nicht beschreiben kann.
Nachbemerkung 2: Joshi (1985) hat mildly context-sensitive als terminus technicus eingeführt und, so bilde ich mir ein, extra nicht weakly genommen, weil dieses Wort im Zusammenhang mit formalen Grammatiken schon eine ganz andere Bedeutung hat, nämlich bei schwacher Äquivalenz. Deswegen finde ich die deutsche Übersetzung schwach kontextsensitiv etwas unglücklich. Hätte man nicht gelinde kontextsensitiv nehmen können?
Nachbemerkung 3: Wo wir schon bei Terminologiekritik sind. Das Begriffspaar kontextfrei und kontextsensitiv hat mich schon immer geärgert. Das klingt so komplementär. Tatsächlich ist aber jede kontextfreie Sprache auch eine kontextsensitive Sprache, siehe Zwiebel. Diese begriffliche Verwirrung ist ein Grund mehr, sich mit der Klasse der kontextsensitiven Sprachen überhaupt nicht mehr zu beschäftigen. *g*
Literatur
Aravind K. Joshi: Tree adjoining grammars: How much context-sensitivity is required to provide reasonable structural descriptions? In: D. Dowty, L. Karttunen und A. Zwicky (Hrsg.), Natural Language Parsing, Cambridge University Press, 1985.
s.a. Literatur zu Teil 1

Pingback: Zwischen Kontextfreiheit und Kontextsensitivität, Teil 1: Crashkurs Simple Range Concatenation Grammars (SRCG) | Texttheater
Nur ganz kurz, später will ich die Artikel gründlicher lesen: laut einem Diagramm in meinem Skript ist PTIME keine Teilmenge von L1.
Interessant, noch ein Gebiet, dem ich mich bisher vollständig verweigert habe. Danke also für diesen Einblick. Bin auf Teil 3 gespannt!
@Herr Rau: An dem Diagramm und womöglich auch Referenzen wäre ich sehr interessiert. Zu der Frage konnte ich nämlich trotz einigen Suchens im Netz nichts finden. Meine E-Mail-Adresse steht im Impressum *liebguck* :-)
Kommt per Mail.
Pingback: Zwischen Kontextfreiheit und Kontextsensitivität, Teil 3: Nicht kontextfreie Grammatiken für Fragmente natürlicher Sprachen | Texttheater